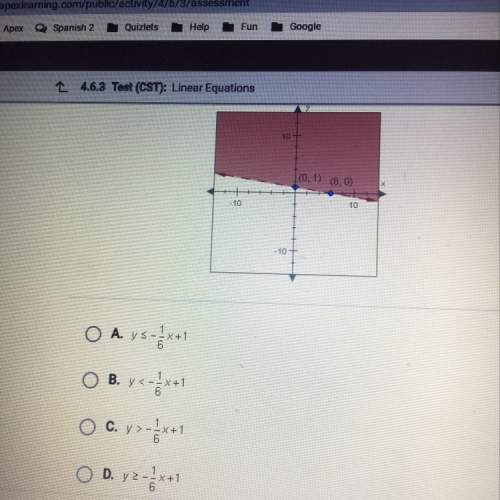
Mathematics, 18.02.2020 20:40, jshhs
(a) Prove using induction that the forward pass of this algorithm always terminates for augmented matrix A ∈ R n×(n+1) . (b) Prove using induction that the backward pass of the algorithm terminates if reached. (c) Prove using induction that the downward pass of the algorithm terminates with an uppertriangular matrix — all the entries below the diagonal are zero. (d) Prove that the algorithm is correct for augmented matrix A ∈ R n×(n+1) for the case when a unique solution exists. To do this, you should first prove a lemma that shows that any solution to the original system of equations remains a solution to the modified system of equations at all iterations of the downward pass of the algorithm, and vice-versa: all solutions of the modified system of equations at all iterations are valid solutions to the original system of equations.

Answers: 1
Other questions on the subject: Mathematics




Mathematics, 22.06.2019 03:00, smiley29162
What is the approximate difference in tenths between √12 and √15?
Answers: 1
Do you know the correct answer?
(a) Prove using induction that the forward pass of this algorithm always terminates for augmented ma...
Questions in other subjects:










Mathematics, 05.05.2020 16:44