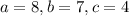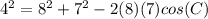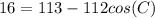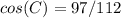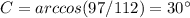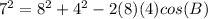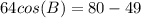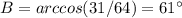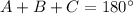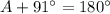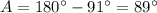Mathematics, 18.07.2019 03:30, IsabelAyshi
Determine whether each triangle should be solved by beginning with the law of sines or the law of cosines. then solve each triangle. round measures of sides and angles to the nearest tenth after calculating. a = 8, b = 7, c = 4 question 3 options: law of cosines; a ≈ 89°, b ≈ 61°, c ≈ 30° law of sines; a ≈ 89°, b ≈ 61°, c ≈ 30° law of sines; a ≈ 30°, b ≈ 61°, c ≈ 89° law of cosines; a ≈ 61°, b ≈ 89°, c ≈ 30°


Answers: 3
Similar questions

Mathematics, 29.08.2019 13:50, noahrdavila1978
Answers: 1

Mathematics, 09.10.2019 04:50, zalbesifki12
Answers: 1

Mathematics, 14.10.2019 23:00, aarhakhanna
Answers: 1
Do you know the correct answer?
Determine whether each triangle should be solved by beginning with the law of sines or the law of co...
Questions in other subjects:


Mathematics, 18.02.2021 18:10

Mathematics, 18.02.2021 18:10






Mathematics, 18.02.2021 18:10

Mathematics, 18.02.2021 18:10