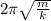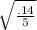Physics, 06.04.2020 19:31, needhelp243435

A 140 g mass is connected to a light spring of force constant 5 N/m that is free to oscillate on a horizontal, frictionless track. The mass is displaced 3 cm from the equilibrium point and released from rest.

(A) Find the period of its motion.
(B) Determine the maximum speed of the block.
(C) What is the maximum acceleration of the block?
(D) Express the position, velocity, and acceleration as functions of time in SI units.

Answers: 1

Show answers

Other questions on the subject: Physics

Physics, 22.06.2019 15:40, dreamdancekay

How does the electric potential energy between two charged particles change if one particle is reduced by a factor of 3? a. increased by a factor of 3 b. it is decreased by a factor of 9 c. it is reduced by a factor of 3 d. it is increased by a factor of 9

Answers: 1

continue

Physics, 22.06.2019 19:00, Drea1385

The particle p starts from rest at point a at time t = 0 and changes its speed thereafter at a constant rate of 2.8g as it follows the horizontal path shown. determine the magnitude and direction of its total acceleration (a) just before point b, (b) just after point b, and (c) as it passes point c. state your directions relative to the x-axis shown (ccw positive) and choose the angle with the smallest magnitude.

Answers: 1

continue

Physics, 22.06.2019 20:20, NNopeNNopeNNope

The base of a 50-meter tower is at the origin; the base of a 50-meter tree is at (0, 50, 0). the ground is flat and the z-axis points upward. the following parametric equations describe the motion of six projectiles each launched at time t = 0 in seconds. (i) r (t) = (50 + t2)k (ii) r (t) = 2t2 j + 2t2k (iii) r (t) = 50 i + 50 j + (50 − t2)k (iv) r (t) = 2t j + (50 − t2)k (v) r (t) = (50 − 2t) i + 2t j + (50 − t)k (vi) r (t) = t i + t j + tk (a) which projectile is launched from the top of the tower and goes downward? at time t = , the projectile hits the ground at point (x, y, z) = . (b) which projectile hits the top of the tree?

Answers: 2

continue

Physics, 22.06.2019 20:20, Webber07

An electron is trapped at a defect in a crystal. the defect may be modeled as a one-dimensional, rigid-walled box of width 1.00 nm. (a) sketch the wavefunctions and probability densities for the n 1 and n 2 states. (b) for the n 1 state, nd the probability of nding the electron between x1 0.15 nm and x2 0.35 nm, where x 0 is the left side of the box. (c) repeat (b) for the n 2 state. (d) calculate the energies in electron volts of the n 1 and n 2 states

Answers: 1

continue

Do you know the correct answer?

A 140 g mass is connected to a light spring of force constant 5 N/m that is free to oscillate on a h...