Mathematics, 22.06.2021 18:00, blackchina71
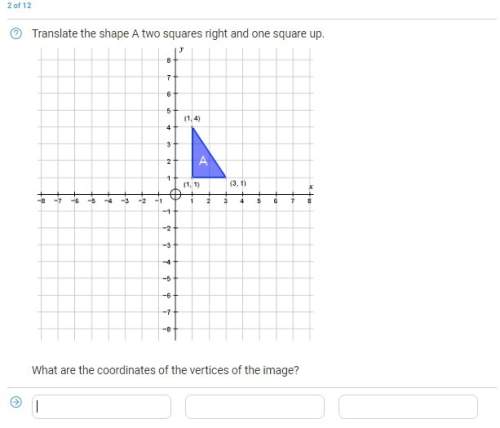
Chaim tried to prove that \triangle UTS \sim \triangle UDE△UTS∼△UDEtriangle, U, T, S, \sim, triangle, U, D, E in the following figure, but his proof is wrong.
What is the first mistake Chaim made in the proof?
Statement Reason
1 \angle SUT \cong \angle EUD∠SUT≅∠EUDangle, S, U, T, \cong, angle, E, U, D Vertical angles are congruent.
2 \overline{ST}\parallel \overline{DE}
ST
∥
DE
start overline, S, T, end overline, \parallel, start overline, D, E, end overline Given
3 \angle UST \cong \angle UED∠UST≅∠UEDangle, U, S, T, \cong, angle, U, E, D Alternate interior angles formed by parallel lines are congruent (2).
4 \triangle UTS \sim \triangle UDE△UTS∼△UDEtriangle, U, T, S, \sim, triangle, U, D, E Angle-angle similarity (1,3)
Choose 1
Choose 1
(Choice A)
A
It is not given that \overline{ST}
ST
start overline, S, T, end overline and \overline{DE}
DE
start overline, D, E, end overline are parallel.
(Choice B)
B
Angles \angle UST∠USTangle, U, S, T and \angle UED∠UEDangle, U, E, D are not alternate interior angles.
(Choice C)
C
The angle-angle criterion establishes congruence, but not similarity.
(Choice D)
D
Chaim didn't match the corresponding vertices correctly in his similarity statement.


Answers: 2
Other questions on the subject: Mathematics



Mathematics, 21.06.2019 22:00, tatertottheyoungin
If x+y+z=0 what is the value of [tex] {x}^{3} + {y}^{3} + {z}^{3} [/tex]
Answers: 2
Do you know the correct answer?
Chaim tried to prove that \triangle UTS \sim \triangle UDE△UTS∼△UDEtriangle, U, T, S, \sim, triangle...
Questions in other subjects:

Biology, 23.04.2020 16:18



Biology, 23.04.2020 16:18

Mathematics, 23.04.2020 16:18