
Mathematics, 26.05.2021 15:10, PrincessIndia
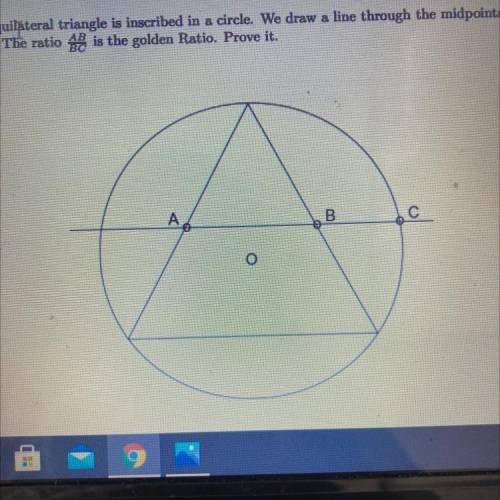
An equilateral triangle is inscribed in a circle. We draw a line through the midpoints of two sides of the triangle. The ratio AB:BC is the golden ratio. Prove it.

Answers: 1
Other questions on the subject: Mathematics

Mathematics, 21.06.2019 15:30, RyannLambertt9722
What is the missing reason in step 5? linear pair postulategivendefinition of complementary anglescongruent complements theorem
Answers: 1


Mathematics, 22.06.2019 02:10, toxsicity
Susan is paying $0.30 per $100 on her $483,000 home in homeowners insurance annually. if her annual homeowners insurance premium is divided into twelve equal monthly installments to be included on each of her monthly mortgage payments of $2,128.00, what is her total monthly payment?
Answers: 2
Do you know the correct answer?
An equilateral triangle is inscribed in a circle. We draw a line through the midpoints of two sides...
Questions in other subjects:


History, 03.03.2022 18:50

Geography, 03.03.2022 18:50

History, 03.03.2022 18:50

Mathematics, 03.03.2022 18:50





Chemistry, 03.03.2022 18:50






