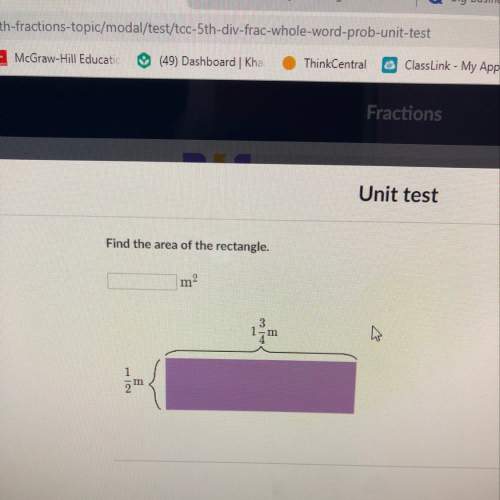
Mathematics, 20.04.2021 22:30, ebzloera
The vertices of rectangle ABCD are A(3, 1), B(-5, 1), C(-5, -3), and D. What are the coordinates of D?

Answers: 1
Other questions on the subject: Mathematics

Mathematics, 21.06.2019 19:00, ktenz
Asmall business produces and sells balls. the fixed costs are $20 and each ball costs $4.32 to produce. each ball sells for $8.32. write the equations for the total cost, c, and the revenue, r, then use the graphing method to determine how many balls must be sold to break even.
Answers: 3

Mathematics, 21.06.2019 19:20, bounce76
When are triangles considered similar? a. corresponding angles are equal andcorresponding sides are proportionalb. corresponding angles are proportional andcorresponding sides are equalc. corresponding angles are equal orcorresponding sides are proportionald. corresponding angles are proportional orcorresponding sides are equal select the best answer from the choices providedmark this and retumsave and exitnext
Answers: 2


Mathematics, 22.06.2019 01:10, hellicuh
Evaluate 8x2 + 9x − 1 2x3 + 3x2 − 2x dx. solution since the degree of the numerator is less than the degree of the denominator, we don't need to divide. we factor the denominator as 2x3 + 3x2 − 2x = x(2x2 + 3x − 2) = x(2x − 1)(x + 2). since the denominator has three distinct linear factors, the partial fraction decomposition of the integrand has the form† 8x2 + 9x − 1 x(2x − 1)(x + 2) = correct: your answer is correct. to determine the values of a, b, and c, we multiply both sides of this equation by the product of the denominators, x(2x − 1)(x + 2), obtaining 8x2 + 9x − 1 = a correct: your answer is correct. (x + 2) + bx(x + 2) + cx(2x − 1).
Answers: 3
Do you know the correct answer?
The vertices of rectangle ABCD are A(3, 1), B(-5, 1),
C(-5, -3), and D. What are the coordinates o...
Questions in other subjects:

Mathematics, 20.12.2020 01:00

English, 20.12.2020 01:00


Mathematics, 20.12.2020 01:00


SAT, 20.12.2020 01:10


Biology, 20.12.2020 01:10