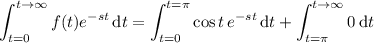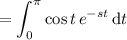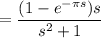Mathematics, 01.10.2019 16:50, debordc17
Definition 7.1.1 laplace transform let f be a function defined for t ≥ 0. then the integral {f(t)} = ∞ e−stf(t) dt 0 is said to be the laplace transform of f, provided that the integral converges. to find {f(t)}. f(t) = cos t, 0 ≤ t < π 0, t ≥ π

Answers: 1
Other questions on the subject: Mathematics

Mathematics, 21.06.2019 13:00, aaron2113
Use this data in the problem below. follow the steps carefully. round to the nearest tenth. lot 3: week 1: 345 week 2: 340 week 3: 400 week 4: 325 step 1. jim enters the data and calculates the average or mean. step 2. jim calculates the deviation from the mean by subtracting the mean from each value. step 3. jim squares each deviation to remove negative signs. step 4. jim sums the squares of each deviation and divides by the count for the variance. step 5. jim takes the square root of the variance to find the standard deviation.
Answers: 2


Mathematics, 21.06.2019 21:30, randallcraig27
Two rectangular prisms have the same volume. the area of the base of the blue prism is 418 4 1 8 square units. the area of the base of the red prism is one-half that of the blue prism. which statement is true?
Answers: 3

Mathematics, 21.06.2019 23:00, Lizethh1
Acaterer knows he will need 60, 50, 80, 40 and 50 dinner napkins on five successive evenings. he can purchase new napkins initially at 25 cents each, after which he can have dirty napkins laundered by a fast one-day laundry service (i. e., dirty napkins given at the end of the day will be ready for use the following day) at 15 cents each, or by a slow two-day service at 8 cents each or both. the caterer wants to know how many napkins he should purchase initially and how many dirty napkins should be laundered by fast and slow service on each of the days in order to minimize his total costs. formulate the caterer’s problem as a linear program as follows (you must state any assumptions you make): a. define all variables clearly. how many are there? b. write out the constraints that must be satisfied, briefly explaining each. (do not simplify.) write out the objective function to be minimized. (do not simplify.)
Answers: 1
Do you know the correct answer?
Definition 7.1.1 laplace transform let f be a function defined for t ≥ 0. then the integral {f(t)} =...
Questions in other subjects:

History, 24.02.2022 01:00

Biology, 24.02.2022 01:00

World Languages, 24.02.2022 01:00


SAT, 24.02.2022 01:00

History, 24.02.2022 01:00


Computers and Technology, 24.02.2022 01:00


Mathematics, 24.02.2022 01:00


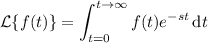
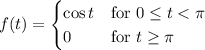
 is given by the definite integral
is given by the definite integral