
Mathematics, 28.03.2021 06:20, GiaTeyy6536
By considering different paths of approach, show that the function has no limit as (x, y)->(0,0). (Function given in attachment)
a. Find the limit as (x, y)->(0,0) along the path y=x for x>0.
b. Find the limit as (x, y)->(0,0) along the path y=x for x<0.

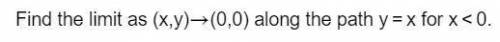

Answers: 3
Other questions on the subject: Mathematics

Mathematics, 21.06.2019 13:30, mallorykay44
Based upon past experience, barry expects no overdrafts. he expects no 2nd copies of statements. barry estimates that he will use network atms about 5 times a month with either bank. barry decides in the end to choose eecu. assuming that both banks provide the necessary services equally well, and based upon the tables of fees given above, how much can barry reasonably expect to save annually by choosing eecu in this case over e-town bank? a. $72 b. $78 c. $144 d. $24
Answers: 2

Mathematics, 21.06.2019 17:00, thicklooney
Which expression is equivalent to 8(k + m) − 15(2k + 5m)?
Answers: 1

Mathematics, 21.06.2019 19:00, garciagang0630
[15 points, algebra 2]simplify the complex fraction and find the restrictions.
Answers: 1

Mathematics, 22.06.2019 00:30, brainist71
L|| m if m? 1=125 and m? 7=50 then m? 5= 5 55 75 105 next question ask for turn it in © 2014 glynlyon, inc. all rights reserved. terms of use
Answers: 3
Do you know the correct answer?
By considering different paths of approach, show that the function has no limit as (x, y)->(0,0)...
Questions in other subjects:

Mathematics, 14.04.2021 01:40



Mathematics, 14.04.2021 01:40

Mathematics, 14.04.2021 01:40

Mathematics, 14.04.2021 01:40

Mathematics, 14.04.2021 01:40


Biology, 14.04.2021 01:40






