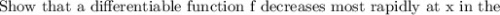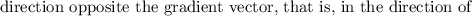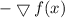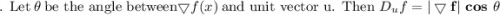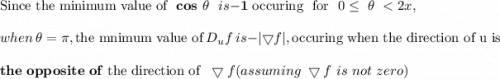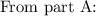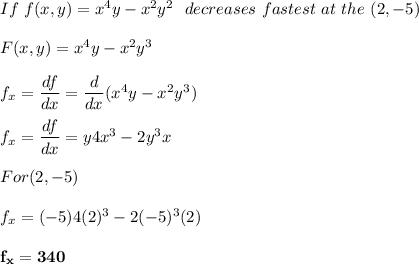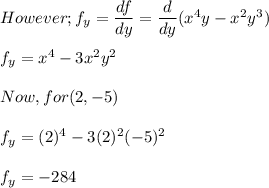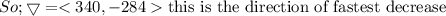Mathematics, 26.03.2021 22:10, meaddestinee
(a) Show that a differentiable function f decreases most rapidly at x in the direction opposite the gradient vector, that is, in the direction of −∇f(x). Let θ be the angle between ∇f(x) and unit vector u. Then Du f = |∇f| cos θ . Since the minimum value of cos θ is -1 occurring, for 0 ≤ θ < 2π, when θ = , the minimum value of Du f is −|∇f|, occurring when the direction of u is the opposite of the direction of ∇f (assuming ∇f is not zero). (b) Use the result of part (a) to find the direction in which the function f(x, y) = x4y − x2y3 decreases fastest at the point (2, −5).

Answers: 3
Other questions on the subject: Mathematics


Mathematics, 22.06.2019 00:00, kittenface3428
28 x 12 + 34 = ? it's for a test that if i fail on i will not proceed into the honor roll society i always dreamed of!me! worth 50 !
Answers: 1

Mathematics, 22.06.2019 00:40, Hjackson24
What is the interquartile range (iqr) of the data set represented by this box plot?
Answers: 3

Mathematics, 22.06.2019 01:20, mickeyo2003
The domain of the following relation: r: {(3, 5), (8, 6), (2, 1), (8, 6)} is (1 point) no domain exists {1, 5, 6} {3, 8, 2, 8} {2, 3, 8}
Answers: 2
Do you know the correct answer?
(a) Show that a differentiable function f decreases most rapidly at x in the direction opposite the...
Questions in other subjects:




Mathematics, 04.10.2019 22:00

Mathematics, 04.10.2019 22:00

Mathematics, 04.10.2019 22:00



Geography, 04.10.2019 22:00