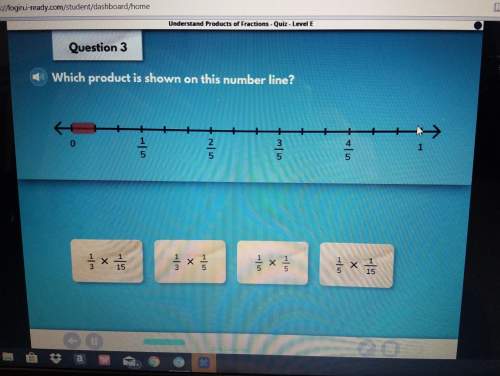
Mathematics, 26.01.2021 23:50, aashna66
Let X be a topological space and let C and U be subsets of X. Define C to be closed if C contains all its limit points and define U to be open if every point p ∈ U has a neighborhood which is contained in U. Assuming these definitions show that the following statements are equivalent for a subset S of X. i) S is closed in X; ii) X – S is open in X; iii) S = [S].

Answers: 3
Other questions on the subject: Mathematics

Mathematics, 21.06.2019 13:30, ellyssabailey2006
Volume of a cylinder with a radius of 13 in and height of 30 in
Answers: 1

Mathematics, 21.06.2019 17:00, tonytashaqua
In triangle opq right angled at p op=7cm, oq-pq=1 determine the values of sinq and cosq
Answers: 1

Mathematics, 21.06.2019 23:00, soldierboy771
What is the length of the midsegment of a trapezoid with bases of length 15 and 25 ?
Answers: 1

Mathematics, 21.06.2019 23:10, ebonsell4910
Larry wants to buy some carpeting for his living room. the length of the room is 4 times the width and the total area of the room is 16 square meters. what is the length of the living room
Answers: 1
Do you know the correct answer?
Let X be a topological space and let C and U be subsets of X. Define C to be closed if C contains al...
Questions in other subjects:


History, 19.08.2019 11:50

Social Studies, 19.08.2019 11:50

History, 19.08.2019 11:50

Biology, 19.08.2019 11:50



English, 19.08.2019 11:50


Biology, 19.08.2019 11:50