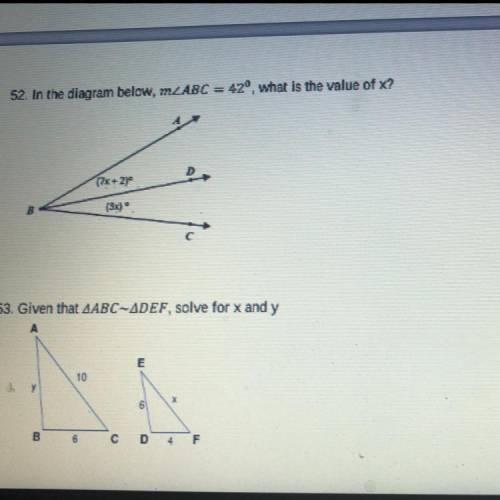
Can someone answer these 2 questions for me?

Farnesene is a sesquiterpene. how many different isomers arising from double-bond isomerizations are possible? g

How does the graph of g(x)=⌊x⌋−3 differ from the graph of f(x)=⌊x⌋? the graph of g(x)=⌊x⌋−3 is the graph of f(x)=⌊x⌋ shifted right 3 units. the graph of g(x)=⌊x⌋−3 is the graph of f(x)=⌊x⌋ shifted up 3 units. the graph of g(x)=⌊x⌋−3 is the graph of f(x)=⌊x⌋ shifted down 3 units. the graph of g(x)=⌊x⌋−3 is the graph of f(x)=⌊x⌋ shifted left 3 units.

Amachine that produces a special type of transistor (a component of computers) has a 2% defective rate. the production is considered a random process where each transistor is independent of the others. (a) what is the probability that the 10th transistor produced is the first with a defect? (b) what is the probability that the machine produces no defective transistors in a batch of 100? (c) on average, how many transistors would you expect to be produced before the first with a defect? what is the standard deviation? (d) another machine that also produces transistors has a 5% defective rate where each transistor is produced independent of the others. on average how many transistors would you expect to be produced with this machine before the first with a defect? what is the standard deviation? (e) based on your answers to parts (c) and (d), how does increasing the probability of an event a↵ect the mean and standard deviation of the wait time until success?