
Mathematics, 23.12.2020 08:20, juliannabartra
I need help with these too questions
Number 1
Number 2

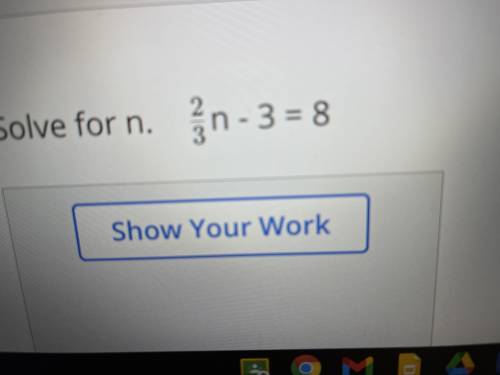

Answers: 3
Other questions on the subject: Mathematics

Mathematics, 21.06.2019 20:30, destinyharris8502
I’m on question 7 it says a covered water tank is in the shape of a cylinder the tank has a 28 inch diameter and a height of 66 inches to the nearest square inch what is the surface area of the water tank
Answers: 2

Mathematics, 21.06.2019 22:30, CatelynBGray
Aaron invested a total of $4,100, some in an account earning 8% simple interest, and the rest in an account earning 5% simple interest. how much did he invest in each account if after one year he earned $211 in interest? select one: a. $200 at 8%, $3,900 at 5% b. $3,200 at 8%, $900 at 5% c. $900 at 8%, $3,200 at 5% d. $3,900 at 8%, $200 at 5%
Answers: 1


Mathematics, 22.06.2019 04:20, heatherballiet866
When booking personal travel by air, one is always interested in actually arriving at one’s final destination even if that arrival is a bit late. the key variables we can typically try to control are the number of flight connections we have to make in route, and the amount of layover time we allow in those airports whenever we must make a connection. the key variables we have less control over are whether any particular flight will arrive at its destination late and, if late, how many minutes late it will be. for this assignment, the following necessarily-simplified assumptions describe our system of interest: the number of connections in route is a random variable with a poisson distribution, with an expected value of 1. the number of minutes of layover time allowed for each connection is based on a random variable with a poisson distribution (expected value 2) such that the allowed layover time is 15*(x+1). the probability that any particular flight segment will arrive late is a binomial distribution, with the probability of being late of 50%. if a flight arrives late, the number of minutes it is late is based on a random variable with an exponential distribution (lamda = .45) such that the minutes late (always rounded up to 10-minute values) is 10*(x+1). what is the probability of arriving at one’s final destination without having missed a connection? use excel.
Answers: 3
Do you know the correct answer?
I need help with these too questions
Number 1
Number 2
...
Number 1
Number 2
...
Questions in other subjects:




History, 14.01.2021 01:30


Spanish, 14.01.2021 01:30



Mathematics, 14.01.2021 01:30






