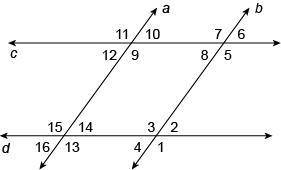
Given ∠4≅∠14, which lines, if any, must be parallel based on the given information? Justify your conclusion. a∥b, Converse of the Same-Side Interior Angles Theorem

a∥b, Converse of the Alternate Interior Angles Theorem

a∥b, Converse of the Corresponding Angles Theorem

not enough information to make a conclusion

In δabc shown below, ∠bac is congruent to ∠bca: triangle abc, where angles a and c are congruent given: base ∠bac and ∠acb are congruent. prove: δabc is an isosceles triangle. when completed (fill in the blanks), the following paragraph proves that line segment ab is congruent to line segment bc making δabc an isosceles triangle. (4 points) construct a perpendicular bisector from point b to line segment ac . label the point of intersection between this perpendicular bisector and line segment ac as point d: m∠bda and m∠bdc is 90° by the definition of a perpendicular bisector. ∠bda is congruent to ∠bdc by the definition of congruent angles. line segment ad is congruent to line segment dc by by the definition of a perpendicular bisector. δbad is congruent to δbcd by the line segment ab is congruent to line segment bc because consequently, δabc is isosceles by definition of an isosceles triangle. 1. corresponding parts of congruent triangles are congruent (cpctc) 2. the definition of a perpendicular bisector 1. the definition of a perpendicular bisector 2. the definition of congruent angles 1. the definition of congruent angles 2. the definition of a perpendicular bisector 1. angle-side-angle (asa) postulate 2. corresponding parts of congruent triangles are congruent (cpctc)