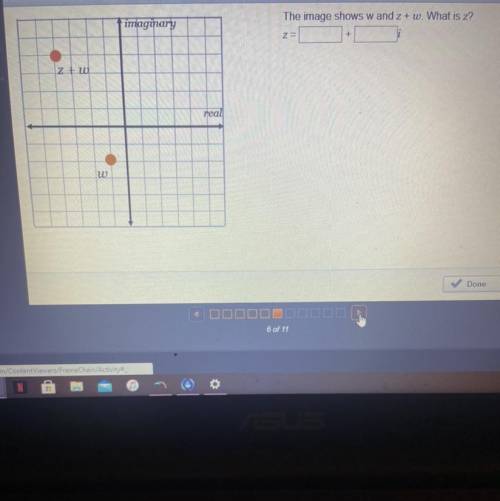
The image shows w and z + w. What is z?
Z=

14. (05.02 lc) what is the value of y in the solution to the following system of equations? (5 points) 2x + y = −4 5x + 3y = −6

Zroms according to the synthetic division below, which of the following statements are true? check all that apply. 352 -2 6 -12 12 2 4 0 i a. (x-3) is a factor of 2x2 - 2x - 12. b. the number 3 is a root of f(x) = 2x2 - 2x - 12. c. (2x2 - 2x - 12) = (x + 3) = (2x + 4) d. (2x2 - 2x-12) - (x-3) = (2x + 4) e. (x+3) is a factor of 2x2 - 2x - 12. o f. the number -3 is a root of fx) = 2x2 - 2x - 12. previous

(20 points) a bank has been receiving complaints from real estate agents that their customers have been waiting too long for mortgage confirmations. the bank prides itself on its mortgage application process and decides to investigate the claims. the bank manager takes a random sample of 20 customers whose mortgage applications have been processed in the last 6 months and finds the following wait times (in days): 5, 7, 22, 4, 12, 9, 9, 14, 3, 6, 5, 15, 10, 17, 12, 10, 9, 4, 10, 13 assume that the random variable x measures the number of days a customer waits for mortgage processing at this bank, and assume that x is normally distributed. 2a. find the sample mean of this data (x ě…). 2b. find the sample variance of x. find the variance of x ě…. for (c), (d), and (e), use the appropriate t-distribution 2c. find the 90% confidence interval for the population mean (îľ). 2d. test the hypothesis that îľ is equal to 7 at the 95% confidence level. (should you do a one-tailed or two-tailed test here? ) 2e. what is the approximate p-value of this hypothesis?