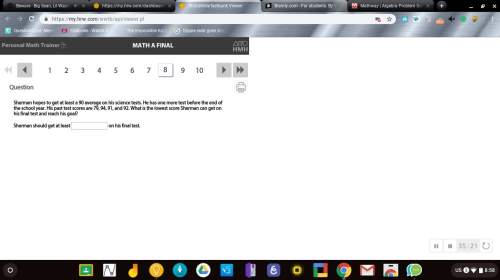
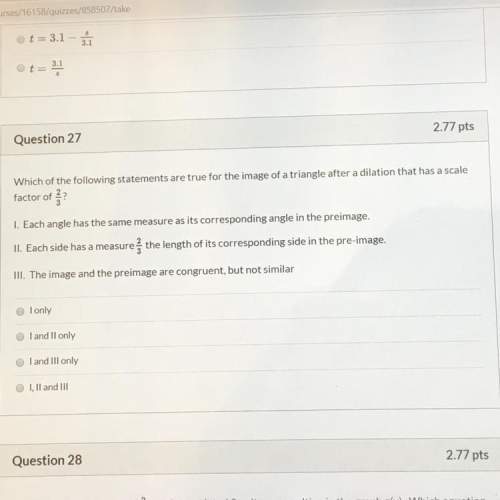
Mathematics, 23.09.2020 18:01, live4dramaoy0yf9
Natural Resources Canada tests new vehicles each year and reports several variables related to fuel consumption for vehicles in different classes. For 2014 they provide data for 512 vehicles that use regular fuel. Two variables reported are carbon dioxide (CO2) emissions and highway fuel consumption. CO2 is measured in grams per kilometer (g/km) and highway fuel consumption measured in liters per 100 kilometers (L/100km). The correlation between these two variables, to six decimal places, was found to be
r = 0.980516.
(a)
Find the equation of the least-squares regression line for predicting CO2 emissions from highway fuel consumption.
(b)
Make a scatterplot of the data with the fitted line.
(c)
How well does the line fit the data? Explain your answer.
(d)
Use the line to predict the value of CO2 for vehicles that consume 11.0 liters per 100 kilometers (L/100km).
Step 1 of 6
(a) Find the equation of the least-squares regression line for predicting CO2 emissions from highway fuel consumption.
The most common method of fitting a line to a scatterplot is least squares. The least-squares regression line minimizes the sum of the squares of the vertical distances of the observed y-values from the line. Given data on an explanatory variable x and a response variable y for n individuals, we can calculate an equation of the least-squares regression line.
We are to find the equation of the least-squares regression line for predicting CO2 emissions from highway fuel consumption for 512 vehicles that use regular fuel. Since CO2 emissions are a result of highway fuel consumption, the CO2 emission is the response variable y [Correct: Your answer is correct.] [seenKey]
response variable y , leaving the highway fuel consumption as the explanatory variable x [Correct: Your answer is correct.] [seenKey]
explanatory variable x
Step 2 of 6
After determining that x represents the highway fuel consumption and y represents the CO2 emissions, we can calculate the equation of the least-squares regression line.
The means and standard deviations of the sample data are x and sx, respectively, for x and y and sy, respectively, for y, and the correlation between x and y is r. The equation of the least-squares regression line of y on x is ? = b0 + b1x with slope
b1 = r sy sx and intercept
b0 = y ? b1x.
You will use software or a calculator with a regression function to find the equation of the least-squares regression line, so the equation given above is in a form that helps understanding but is not efficient for calculation by hand.
Remembering the general form
? = b0 + b1x,
first give the slope correct to five decimal places.
b1 =
Then, give the intercept correct to five decimal places.
b0 =

Answers: 3
Other questions on the subject: Mathematics

Mathematics, 21.06.2019 13:30, jasarochel
The variable z is directly proportional to x, and inversely proportional to y. when x is 4 and y is 13, z has the value 1.2307692307692. what is the value of z when x= 9, and y= 20
Answers: 2


Do you know the correct answer?
Natural Resources Canada tests new vehicles each year and reports several variables related to fuel...
Questions in other subjects:






History, 18.12.2020 07:00

Biology, 18.12.2020 07:00

English, 18.12.2020 07:00