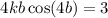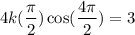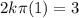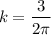Mathematics, 29.07.2020 03:01, cathydaves
Consider the curve of the form y(t) = ksin(bt2) . (a) Given that the first critical point of y(t) for positive t occurs at t = 1 tells us that y '(0) = 1 y(0) = 1 y '(1) = 0 y(1) = 0 Given that the derivative value of y(t) is 3 when t = 2 tells us that y '(3) = 2 y '(0) = 2 y '(2) = 0 y '(2) = 3 (b) Find dy dt = kcos(bt2)·b2t (c) Find the exact values for k and b that satisfy the conditions in part (a). Note: Choose the smallest positive value of b that works.

Answers: 1
Other questions on the subject: Mathematics


Mathematics, 21.06.2019 19:00, nicolemaefahey
How do i start to solve? would appreciate a walk-thru! a bird sitting 16ft above the ground in an apple tree dislodges an apple. after how many seconds does the apple land on the ground? (assuming that no branches will interfere with it's fall)
Answers: 1

Mathematics, 21.06.2019 19:30, vanessagallion
Evaluate 3(a + b + c)squared for a = 2, b = 3, and c = 4. a. 54 b. 243 c.729 add solution .
Answers: 1

Mathematics, 22.06.2019 01:20, ctyrector
Anita has a success rate of 80% on free throws in basketball. she wants to know the estimated probability that she can make exactly four of five free throws in her next game. how can she simulate this scenario? categorize each simulation of this scenario as correct or incorrect.
Answers: 2
Do you know the correct answer?
Consider the curve of the form y(t) = ksin(bt2) . (a) Given that the first critical point of y(t) fo...
Questions in other subjects:


Advanced Placement (AP), 19.12.2020 01:00

German, 19.12.2020 01:00


Mathematics, 19.12.2020 01:00




Business, 19.12.2020 01:00



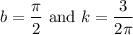
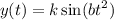
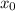 which lies in the domain of f where the derivative is 0.
which lies in the domain of f where the derivative is 0.![y'(t)=\frac{d}{dt}[k \sin (bt^2)]\\ y'(t)=k\frac{d}{dt}[\sin (bt^2)]](/tpl/images/0714/5492/bcd93.png)
![y'(t)=k \cos (bt^2)(\frac{d}{dt}[bt^2])\\ y'(t)=k\cos(bt^2)(b2t)\\ y'(t)= kb2t\cos(bt^2)](/tpl/images/0714/5492/e6dee.png)
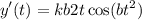

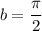
![$\therefore kb2(2)\cos [b(2)^2]=3$](/tpl/images/0714/5492/dd1ee.png)