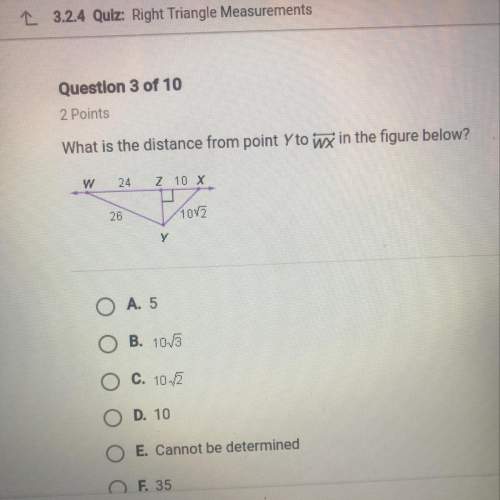
Mathematics, 27.06.2020 19:01, lin550
The admissions officer at a small college compares the scores on the Scholastic Aptitude Test (SAT) for the school's in-state and out-of-state applicants. A random sample of 8 in-state applicants results in a SAT scoring mean of 1144 with a standard deviation of 25. A random sample of 17 out-of-state applicants results in a SAT scoring mean of 1200 with a standard deviation of 26. Using this data, find the 90% confidence interval for the true mean difference between the scoring mean for in-state applicants and out-of-state applicants. Assume that the population variances are not equal and that the two populations are normally distributed. Step 1 of 3 : Find the point estimate that should be used in constructing the confidence interval

Answers: 3
Other questions on the subject: Mathematics

Mathematics, 21.06.2019 15:00, asianpatriot7375
The sixth grade art students are making a mosaic using tiles in the shape of right triangles. each tile has leg measures of 3 centimeters and 5 centimeters. i f there are 200 tiles in the mosaic what is the area of the mosaic.
Answers: 1

Mathematics, 21.06.2019 18:30, mikey8510
The median of a data set is the measure of center that is found by adding the data values and dividing the total by the number of data values that is the value that occurs with the greatest frequency that is the value midway between the maximum and minimum values in the original data set that is the middle value when the original data values are arranged in order of increasing (or decreasing) magnitude
Answers: 3


Mathematics, 21.06.2019 21:30, gonzalezashley152
In a test for esp (extrasensory perception), the experimenter looks at cards that are hidden from the subject. each card contains either a star, a circle, a wave, a cross or a square.(five shapes) as the experimenter looks at each of 20 cards in turn, the subject names the shape on the card. when the esp study described above discovers a subject whose performance appears to be better than guessing, the study continues at greater length. the experimenter looks at many cards bearing one of five shapes (star, square, circle, wave, and cross) in an order determined by random numbers. the subject cannot see the experimenter as he looks at each card in turn, in order to avoid any possible nonverbal clues. the answers of a subject who does not have esp should be independent observations, each with probability 1/5 of success. we record 1000 attempts. which of the following assumptions must be met in order to solve this problem? it's reasonable to assume normality 0.8(1000), 0.2(1000)%30 approximately normal 0.8(1000), 0.2(1000)% 10 approximately normal srs it is reasonable to assume the total number of cards is over 10,000 it is reasonable to assume the total number of cards is over 1000
Answers: 1
Do you know the correct answer?
The admissions officer at a small college compares the scores on the Scholastic Aptitude Test (SAT)...
Questions in other subjects:

Physics, 30.10.2019 06:31

Mathematics, 30.10.2019 06:31


Physics, 30.10.2019 06:31

Mathematics, 30.10.2019 06:31




History, 30.10.2019 06:31

Mathematics, 30.10.2019 06:31