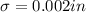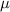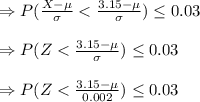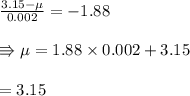Mathematics, 23.06.2020 17:01, seider8952
In a grinding operation, there is an upper specification of 3.150 in. on a dimension of a certain part after grinding. Suppose that the standard deviation of this normally distributed dimension for parts of this type ground to any particular mean dimension LaTeX: \mu\:is\:\sigma=.002 μ i s σ = .002 in. Suppose further that you desire to have no more than 3% of the parts fail to meet specifications. What is the maximum (minimum machining cost) LaTeX: \mu μ that can be used if this 3% requirement is to be met?

Answers: 3
Other questions on the subject: Mathematics

Mathematics, 21.06.2019 13:00, brialevy2283
Find the total area for the regular pyramid ( follow the answer set up in the picture)
Answers: 1

Mathematics, 21.06.2019 16:00, RyannLambertt9722
On saturday morning, calls arrive at ticketmaster at a rate of 108 calls per hour. what is the probability of fewer than three calls in a randomly chosen minute?
Answers: 1

Mathematics, 21.06.2019 17:00, Tymere2011
Which measure is equivalent to 110 ml? 0.0110 l 0.110 l 1.10 l 11,000 l
Answers: 2

Mathematics, 21.06.2019 23:30, Krazyyykiddd
Xy x xy if a and b are positive integers such that a*b=9 and b*a=72 what is the value of a/b
Answers: 3
Do you know the correct answer?
In a grinding operation, there is an upper specification of 3.150 in. on a dimension of a certain pa...
Questions in other subjects:


History, 14.05.2021 20:10


Chemistry, 14.05.2021 20:10

Mathematics, 14.05.2021 20:10


Mathematics, 14.05.2021 20:10

Mathematics, 14.05.2021 20:10


Mathematics, 14.05.2021 20:10