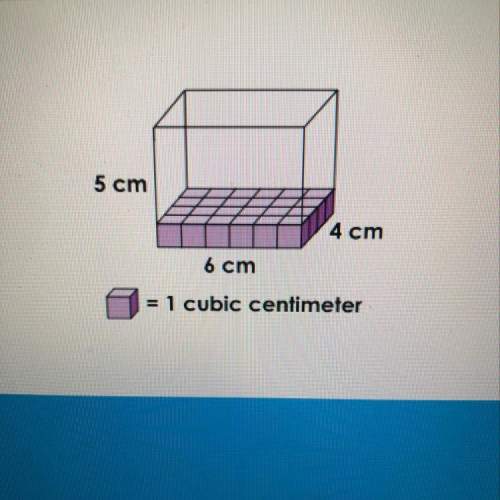
Mathematics, 05.05.2020 06:00, chris1848
Consider a set A = {a1, . . . , an} and a collection B1, . . . , Bm of subsets of A (i. e. Bi ⊆ A for each i.) We say that a set H ⊆ A is a hitting set for the collection B1, . . . , Bm if H contains at least one element from each Bi - that is, if H T Bi is not empty for each i (so H hits all the sets Bi .) We now define the hitting set problem as follows. We are given a set A = {a1, . . . , an}, a collection B1, . . . , Bm of subsets of A, and a number k. We are asked: Is there a hitting set H ⊆ A for B1, . . . , Bm so that the size of H is at most k? Prove that hitting set is NP-complete.

Answers: 3
Other questions on the subject: Mathematics

Mathematics, 21.06.2019 19:30, tyeni2crazylolp7a3hk
If chord ab is congruent to chord cd, then what must be true about ef and eg?
Answers: 1


Mathematics, 21.06.2019 21:30, kyandrewilliams1
Alcoa was $10.02 a share yesterday. today it is at $9.75 a share. if you own 50 shares, did ou have capital gain or loss ? how much of a gain or loss did you have ? express the capital gain/loss as a percent of the original price
Answers: 2

Mathematics, 21.06.2019 23:00, slonekaitlyn01
Shared decision making is always a positive strategy to take
Answers: 1
Do you know the correct answer?
Consider a set A = {a1, . . . , an} and a collection B1, . . . , Bm of subsets of A (i. e. Bi ⊆ A fo...
Questions in other subjects:


Business, 30.09.2019 03:00

Social Studies, 30.09.2019 03:00



History, 30.09.2019 03:00

Mathematics, 30.09.2019 03:00