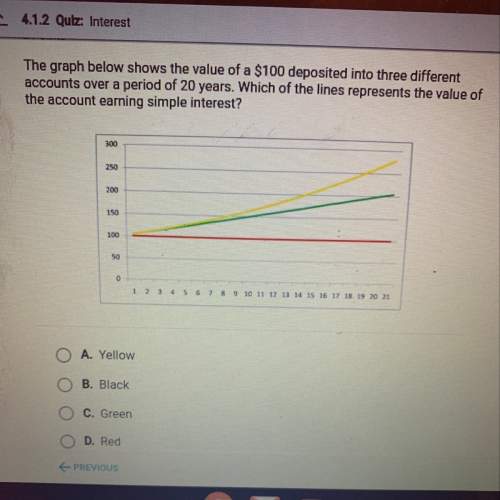
Mathematics, 09.04.2020 23:36, chrisd2038
F(x) = b^x represents exponential growth when b>1 and exponential decay when 0 < b < 1.
What happens when b = 1? Why?

Answers: 1
Other questions on the subject: Mathematics


Mathematics, 22.06.2019 00:00, andreaolvera
Add, subtract, multiply, or divide as indicated. list any restrictions for the variable(s) and simplify the answers when possible. 1) x-2 / x+5 + 3x / 2x-1 2) x+6 / x-6 - x^2 / x+6 3) x+9 / x-4 + x+2 / x^2-11x+28 4) x / x^2-64 + 11 / 2x^2+11x-40 5) 5 / x + 11 / x-3 - x-4 / x^2+2x-15
Answers: 1

Mathematics, 22.06.2019 01:00, sierraseideman1023
X^2/100+y^2/25=1 the length of the major axis is: a)5 b)10 c)20
Answers: 3

Mathematics, 22.06.2019 07:30, BryantDream
N=1,2,3,4,5 a n= 9,18,36,72,144 a recursive rule for the sequence is: f(1)= and f(n)= for n≥2. an explicit rule for the sequence is: f(n)= find a recursive rule and an explicit for the geometric sequence. 768,192,48,12,3,… a recursive rule for the sequence is: f(1)= and f(n)= for n≥2. an explicit rule for the sequence is: f(n)=∙ -1. concept 3: deriving the general forms of geometric sequence rules your turn use the geometric sequence to find a recursive rule and an explicit rule for any geometric sequence. 4,8,16,32,64,… recursive rule for the geometric sequence: f(1)= and f(n)=f(n-1)∙ for n≥2. recursive rule for any geometric sequence: given f(1),f(n)=f(n-1)∙ for n≥2. explicit rule for the geometric sequence: f(n)=∙-1. explicit rule for any geometric sequence: f(n)=∙-1 concept 4: constructing a geometric sequence given two terms your turn find an explicit rule for the sequence using subscript notation. the third term of a geometric sequence is 1/48 and the fifth term of the sequence is 1/432. all the terms of the sequence are positive. the explicit rule for the geometric sequence is
Answers: 2
Do you know the correct answer?
F(x) = b^x represents exponential growth when b>1 and exponential decay when 0 < b < 1.
Questions in other subjects:

Mathematics, 08.10.2019 13:30








English, 08.10.2019 13:30