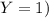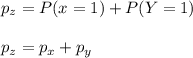Mathematics, 24.03.2020 16:54, makylahoyle
(4.1.4) Let X and Y be Bernoulli random variables. Let Z = X + Y. a. Show that if X and Y cannot both be equal to 1, then Z is a Bernoulli random variable. b. Show that if X and Y cannot both be equal to 1, then pZ = pX + pY. c. Show that if X and Y can both be equal to 1, then Z is not a Bernoulli random variable.

Answers: 2
Other questions on the subject: Mathematics

Mathematics, 21.06.2019 14:30, smith3mgy
Simonne used the following steps to simplify the given expression. 12 - 3(-2x + 4) step 1: 12 + (–3)·(–2x) + (–3)·(4) step 2: 12 + 6x + (–12) step 3: 12 + (–12) + 6x step 4: 0 + 6x step 5: 6x what property of real numbers was used to transition from step 3 to step 4? a. identity property of addition b. inverse property of addition c. associative property of addition d. commutative property of addition
Answers: 1

Mathematics, 21.06.2019 17:00, reaunnatowns
High schoolmathematics 5 points keith is the leading goal scorer for a team in an ice hockey league. last season, he scored 42 goals in 82 games. assuming he scores goals at a constant rate, what is the slope of the line that represents this relationship if the number of games is along the x-axis and the number of goals is along the y-axis?
Answers: 1

Mathematics, 21.06.2019 18:30, alizeleach0123
Which representation has a constant of variation of -2.5
Answers: 1

Mathematics, 22.06.2019 00:00, buddyclayjohnson
Which of these angles are supplementary? a. 100o and 90o b. 78o and 102o c. 54o and 146o d. 12o and 78o
Answers: 1
Do you know the correct answer?
(4.1.4) Let X and Y be Bernoulli random variables. Let Z = X + Y. a. Show that if X and Y cannot bot...
Questions in other subjects:

Mathematics, 29.10.2019 12:31


Arts, 29.10.2019 12:31

Mathematics, 29.10.2019 12:31




English, 29.10.2019 12:31

Mathematics, 29.10.2019 12:31


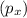 and Y ~ Bernoulli
and Y ~ Bernoulli 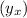
 or
or 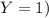
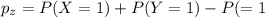 and
and