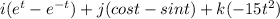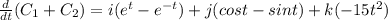Let c1(t) = eti + (sin(t))j + t3k and c2(t) = e−ti + (cos(t))j − 6t3k. Find the stated derivatives in two different ways to verify the differentiation rules. d dt [c1(t) + c2(t)]

(mc 02.03) what set of reflections and rotations would carry rectangle abcd onto itself? reflect over the y-axis, reflect over the x-axis, rotate 180° rotate 180°, reflect over the x-axis, reflect over the line y=x reflect over the x-axis, rotate 180°, reflect over the x-axis rotate 180, reflect over the y-axis, reflect over the line y=x

Which expression shows the sum of the polynomials with like terms grouped together

Apoll is being conducted at a mall nothingto obtain a sample of the population of an entire country. what is the frame for this type of​ sampling? who would be excluded from the survey and how might this affect the results of the​ survey? what is the frame for this type of​ sampling? a. the frame is people who need new clothes. b. the frame is people who shop at the mall. c. the frame is people who like to shop. d. the frame is the entire population of the country. who would be excluded from the survey and how might this affect the results of the​ survey? a. any person that does not need new clothes is excluded. this could result in sampling bias due to undercoverage. b. any person who does not shop at the mall is excluded. this could result in sampling bias due to undercoverage. c. any person who does not shop at the mall is excluded. this could result in nonresponse bias due to people not participating in the poll. d. there is nobody that is being excluded from the survey.