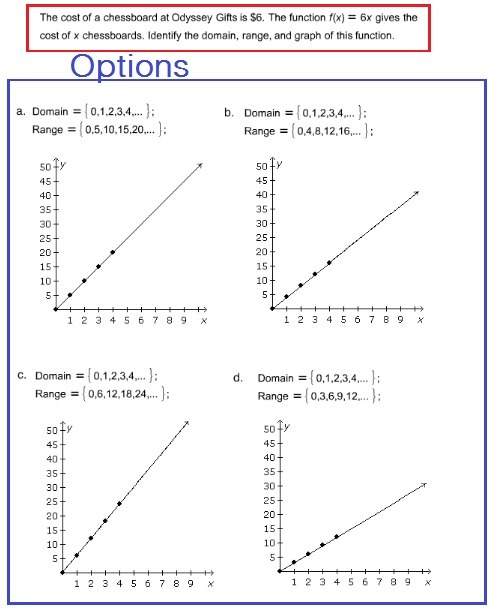
Mathematics, 13.03.2020 18:53, jpsaad00
Let F be a planar vector field and again consider an annular region A as in the previous problem. Suppose that F has no equilibria and that F points inward along the boundary of the annulus, as before. (a) Prove there is a closed orbit in A. (Notice that the hypothesis is weaker than in the previous problem.)(b) If there are exactly seven closed orbits in A, show that one of them has orbits spiraling toward it from both sides.

Answers: 1
Other questions on the subject: Mathematics


Mathematics, 21.06.2019 18:30, issagirl05
Find the exact value of each of the following. in each case, show your work and explain the steps you take to find the value. (a) sin 17π/6 (b) tan 13π/4 (c) sec 11π/3
Answers: 2

Do you know the correct answer?
Let F be a planar vector field and again consider an annular region A as in the previous problem. Su...
Questions in other subjects:





Advanced Placement (AP), 09.04.2020 22:03

Mathematics, 09.04.2020 22:03

Mathematics, 09.04.2020 22:03

Mathematics, 09.04.2020 22:03