Mathematics, 29.11.2019 01:31, Animallover100
Let x1, . . be independent random variables with the common distribution function f, and suppose they are independent of n, a geometric random variable with parameter p. let m = max(x1, . . ,xn). (a) find p{m … x} by conditioning on n. (b) find p{m … x|n = 1}. (c) find p{m … x|n > 1}. (d) use (b) and (c) to rederive the probability you found in (a).

Answers: 1
Other questions on the subject: Mathematics

Mathematics, 21.06.2019 16:50, Chartwig4831
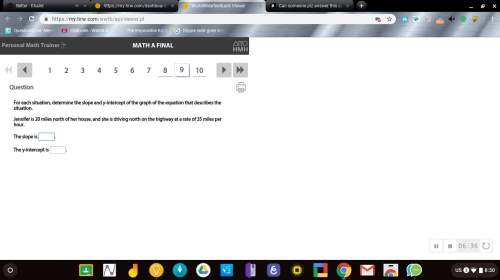
For the equations below which statement is true ? -2x=14 6x=-42
Answers: 1

Mathematics, 21.06.2019 19:30, ellarose0731
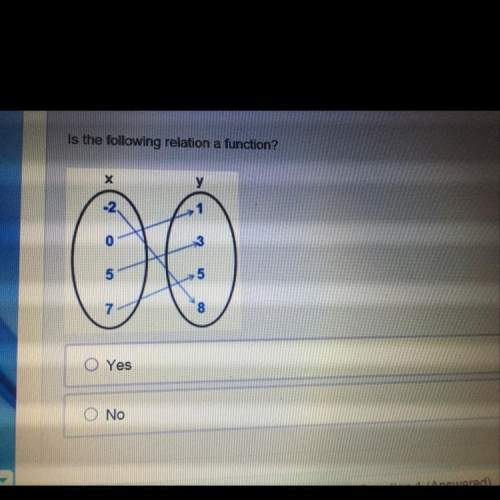
Hi, can anyone show me how to do this problem? 100 points for this. in advance
Answers: 2

Mathematics, 21.06.2019 20:30, amauris77748
There are 45 questions on your math exam. you answered 810 of them correctly. how many questions did you answer correctly?
Answers: 3

Mathematics, 21.06.2019 21:00, villanuevajose95
A. s.a.! this is a similarity in right triangles. next (solve for x)a.) 12b.) 5c.) 12.5d.) [tex] 6\sqrt{3} [/tex]
Answers: 2
Do you know the correct answer?
Let x1, . . be independent random variables with the common distribution function f, and suppose th...
Questions in other subjects:


Social Studies, 08.10.2019 18:00

Mathematics, 08.10.2019 18:00


Mathematics, 08.10.2019 18:00


Mathematics, 08.10.2019 18:00


Business, 08.10.2019 18:00