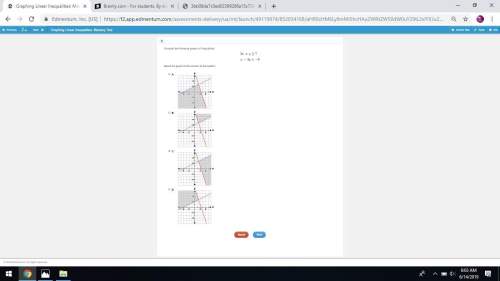
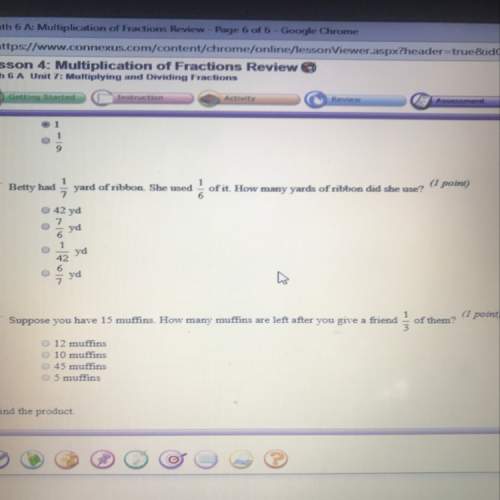
Mathematics, 26.11.2019 06:31, 22millt
Suppose that (n, e) is an rsa encryption key, with n = pq, where p and q are large primes and gcd(e, (p − 1)(q − 1)) = 1. furthermore, suppose that d is an inverse of e modulo (p − 1)(q − 1). suppose that c ≡ me (mod pq). in the text we showed that rsa decryption, that is, the congruence cd ≡ m (mod pq) holds when gcd(m, pq) = 1. show that this decryption congruence also holds when gcd(m, pq) > 1. [hint: use congruences modulo p and modulo q and apply the chinese remainder theorem.]

Answers: 2
Other questions on the subject: Mathematics

Mathematics, 21.06.2019 16:30, hector87
The label on the car's antifreeze container claims to protect the car between ? 40°c and 125°c. to convert celsius temperature to fahrenheit temperature, the formula is c = 5 over 9 (f ? 32). write and solve the inequality to determine the fahrenheit temperature range at which this antifreeze protects the car. ? 40 > 5 over 9 (f ? 32) > 125; ? 40 > f > 257 ? 40 < 5 over 9 (f ? 32) < 125; ? 40 < f < 257 ? 40 < 5 over 9 (f ? 32); ? 40 < f 5 over 9 (f ? 32) < 125; f < 257
Answers: 2

Mathematics, 21.06.2019 22:00, hannahpalmario
The customer price index(cpi), which measures the cost of a typical package of customer goods, was 208.8 in 2011 and 244.1 in 2016.let x=11 corresponding to the year 2011 an estimate to cpi into 2013 and 2014. assume that the data can be modeled by a straight line and the trend to continue idenfinitely. use data points to find such a line and then estimate the requested quantities
Answers: 1

Mathematics, 22.06.2019 03:00, samjohnson3637
What is the answer to question 11? richard simplified an expression in three steps, as shown taking 04.10 segment one exam part one (flvs)
Answers: 3

Mathematics, 22.06.2019 04:00, jenniferleeross53
If the equation of a perpendicular bisector of a triangle is y = 2x + 7, what is the slope of the side that it is bisecting? explain how you know.
Answers: 1
Do you know the correct answer?
Suppose that (n, e) is an rsa encryption key, with n = pq, where p and q are large primes and gcd(e,...
Questions in other subjects:


Chemistry, 22.10.2019 14:00

Biology, 22.10.2019 14:00

Health, 22.10.2019 14:00

Chemistry, 22.10.2019 14:00

History, 22.10.2019 14:00



Biology, 22.10.2019 14:50

English, 22.10.2019 14:50