
Mathematics, 01.11.2019 07:31, joannachavez12345
In section 1.3 we saw that the autonomous differential equation m dv dt = mg − kv, where k is a positive constant and g is the acceleration due to gravity, is a model for the velocity v of a body of mass m that is falling under the influence of gravity. because the term −kv represents air resistance, the velocity of a body falling from a great height does not increase without bound as time t increases. use a phase portrait of the differential equation to find the limiting, or terminal, velocity of the body. lim v(t -> infinity)=

Answers: 2
Other questions on the subject: Mathematics


Mathematics, 21.06.2019 17:30, cecelia090
Any is very appreciated! (picture is provided below)not sure how to do this at all won't lie
Answers: 1

Do you know the correct answer?
In section 1.3 we saw that the autonomous differential equation m dv dt = mg − kv, where k is a posi...
Questions in other subjects:

Mathematics, 06.09.2020 03:01

Mathematics, 06.09.2020 03:01


Mathematics, 06.09.2020 03:01

Mathematics, 06.09.2020 03:01


Mathematics, 06.09.2020 03:01



Mathematics, 06.09.2020 03:01


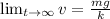

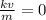


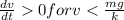

 is stable
is stable



