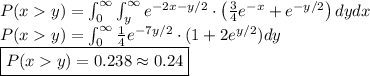Mathematics, 18.09.2019 05:30, ItzMeEmilyyyy
Suppose that we are waiting for two events a and b to occur. x = the time until event a occurs and y = the time until event b occurs. we model the probability distribution of the two times with the joint density
f(x, y) = e^(−2x− y/2) [3/4 e^−x + e^−y/2 ]
for x > 0 and y > 0.
(a) what is the probability that x < 1 but y > 1?
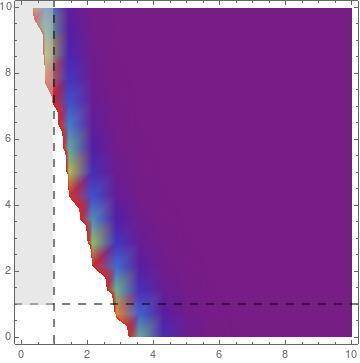
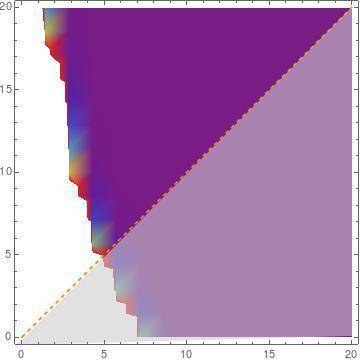
(b) what is the probability that x > y ?

Answers: 3
Other questions on the subject: Mathematics

Mathematics, 21.06.2019 19:10, hannahbannana98
If i have 20$ and i gave 5$ away how much i got
Answers: 1

Mathematics, 21.06.2019 19:30, leilanimontes714
Solve the following simultaneous equation by using an algebraic method (either substitution or elimination) 2x + 3y=-4 4x-y=11
Answers: 1

Mathematics, 21.06.2019 22:00, lraesingleton
What is the solution to the division problem below x3+x2-11x+4/x+4
Answers: 2

Mathematics, 21.06.2019 23:30, michaellangley
Consider the input and output values for f(x) = 2x - 3 and g(x) = 2x + 7. what is a reasonable explanation for different rules with different input values producing the same sequence?
Answers: 1
Do you know the correct answer?
Suppose that we are waiting for two events a and b to occur. x = the time until event a occurs and y...
Questions in other subjects:


Mathematics, 04.04.2020 12:26


Mathematics, 04.04.2020 12:26

Chemistry, 04.04.2020 12:26






 0.45
0.45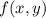 this is:
this is:![P(x\in [x_0, x_1], y\in [y_0, y_1])=\int_{x_0}^{x_1}\int_{y_0}^{y_1}f(x,y)dydx](/tpl/images/0238/8105/2bb33.png) (1)
(1)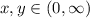 .
.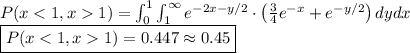
 are given by the function
are given by the function  and notice (second figure attached) that the region where
and notice (second figure attached) that the region where 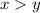 is below the function. Therefore
is below the function. Therefore 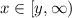 :
: