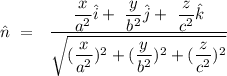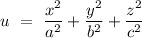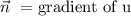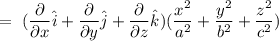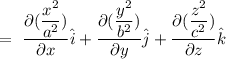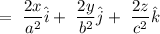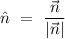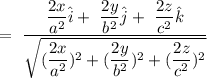Mathematics

Mathematics, 14.09.2019 08:30, Dylan5857

The equation giving a family of ellipsoids is u = (x^2)/(a^2) + (y^2)/(b^2) + (z^2)/(c^2) . find the unit vector normal to each point of the surface of this ellipsoids.

answer

Answers: 2

Show answers

Similar questions

Предмет

Mathematics, 29.08.2019 22:10, jaylabeatty44

11. at the halfway point through these questions, you probably need a break. what should i do? a) give a really hard problem that is so hard you won't even try it, thus giving you a break b) give a really long problem that will keep you from trying the next 9 problems too soon, thus giving you a break c) tell you the next 5 questions are based on material you have still need to read about, thus giving you a break from these questions for a while d) give everyone 4 free points. 12. (t f) if the divergence of a vector field f(z.y,) is zero, then the curl must be the zero vector as well 13. (t f) the function f(x, y) = e-# + v5 is a potential function for the vector field f 0, then vf ,0 for any c > 0. 16. when simplified, the value of the derivative of f(r, y) = e-z* at the point (1,1) in the direction of the vector is in the form a/b, where a and b are integers. enter their sum a + b 17. (t f) suppose you know that vf(a, 6) = and that the directional derivative of f in the direction from the point (a,b) to the point (a+1,b+1) is positive. then the directional derivative of f in the direction from the point (a, b) to the point (a-1,b-1) must be negative. 18. suppose f(r,y) is known to be a conservative vector field. then all of the following statements except one must be true. which one is not definitely true? a)vx f bv f 0 c) if c goes from (1,0) to (-1,0) around the top half of the unit eircle, while c2 goes from (1,0) to (-1,0) around the bottom half of the unit circle, then f-dr= f di d) there is a scalar function f(z, y) such that f = vf.

Answers: 3

Предмет

Physics, 05.10.2019 01:10, Naysa150724

Arocket moves downwards with constant speed of 800 m/s along a parabolic path. the equation of the path is yy = 600 − xx2 121. when the rocket is at a point pp, the angle thetatheta measured counterclockwise from the to this point on the path is 60o. find: (a) the and coordinates of the point pp. (b) plot the path to scale (use matlab to do this). draw the normal and tangential unit vectors �⃗ and �⃗ at the point pp. what is the angle between the tangential unit vector �⃗ and the positive direction of the

Answers: 3

Do you know the correct answer?

The equation giving a family of ellipsoids is u = (x^2)/(a^2) + (y^2)/(b^2) + (z^2)/(c^2) . find the...

Questions in other subjects:

Konu

Social Studies, 03.10.2019 11:30

Biofeedback promotes in order to treat health conditions. a. focusing the mind b. the use of medication c. hypnosis d. exercise

Konu

History, 03.10.2019 11:30

Which event did president john f. kennedy blame on the failures of the eisenhower administration?...

Konu

Social Studies, 03.10.2019 11:30

Read the following excerpt from the communist manifesto by karl marx and friedrich engels. how has their prediction of communist revolutions played out in real world events?...

Konu

Chemistry, 03.10.2019 11:30

2n2h4 + n2o4 → 3n2 + 4h2o how many grams of n2h4 will be consumed by 92 g of n2o4? 16 g 128 g 64 g 32 g...

Konu

Biology, 03.10.2019 11:30

Fish eating birds land on rocky islands...

Konu

Mathematics, 03.10.2019 11:30

6^(x-8) =730 need to show work, show me how...

Konu

Physics, 03.10.2019 11:30

What are substances that have the same composition, but different structures, known as? a. ions c. allotropes b. covalent twins d. phenotypes...

Konu

Advanced Placement (AP), 03.10.2019 11:30

Patrick has assets that total $9,500. his liabilities total $1,900. which expression will find patrick’s net worth?...

Konu

Biology, 03.10.2019 11:30

Which of the following si not a protein function? insulation, transportation, support, defense, motion...

Konu

Physics, 03.10.2019 11:30

Which lunar phase follows a waxing crescent phase? a. full b. new c. first quarter d. third quarter...

Other tasks in the category: Mathematics More task