
Mathematics, 22.01.2020 00:31, cathydaves
Show that if x ∼ geom(p) then p(x = n + k|x > n) = p(x = k), for every n, k ≥ 1. this one of the ways to define the memoryless property of the geometric distribution. it states the following: given that there are no successes in the first n trials, the probability that the first success comes at trial n + k is the same as the probability that a freshly started sequence of trials yields the first success at trial k.

Answers: 1
Other questions on the subject: Mathematics

Mathematics, 21.06.2019 20:30, meowmeowcow
Given: klmn is a parallelogram m? n=3m? k, lf ? kn , ld ? nm kf=2 cm, fn=4 cm find: lf, ld
Answers: 1

Mathematics, 21.06.2019 21:00, recon12759
Is there an x intercept in the equation 60*1.15^x
Answers: 3
Do you know the correct answer?
Show that if x ∼ geom(p) then p(x = n + k|x > n) = p(x = k), for every n, k ≥ 1. this one of the...
Questions in other subjects:





Health, 14.04.2020 18:02






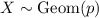 ,
, 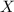 has PMF
has PMF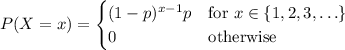
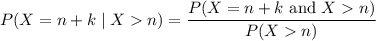
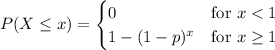
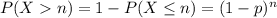
 and
and 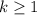 , then it's always true that
, then it's always true that 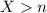 , so
, so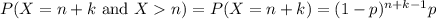
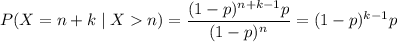
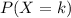 according to the PMF.
according to the PMF.



