Mathematics, 04.07.2019 19:00, gabegabemm1
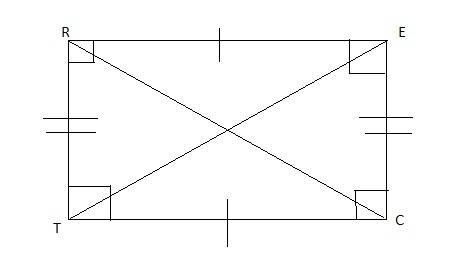
Spencer wrote the following paragraph proof showing that rectangles are parallelograms with congruent diagonals. quadrilateral r e c t is shown with right angles at each of the four corners. segments e r and c t have single hash marks indicating they are congruent while segments e c and r t have two arrows indicating they are parallel. segments e t and c r are drawn. according to the given information, quadrilateral rect is a rectangle. by the definition of a rectangle, all four angles measure 90°. segment er is parallel to segment ct and segment ec is parallel to segment rt by the quadrilateral rect is then a parallelogram by definition of a parallelogram. now, construct diagonals et and cr. because rect is a parallelogram, opposite sides are congruent. therefore, one can say that segment er is congruent to segment ct. segment tr is congruent to itself by the reflexive property of equality. the side-angle-side (sas) theorem says triangle ert is congruent to triangle ctr. and because corresponding parts of congruent triangles are congruent (cpctc), diagonals et and cr are congruent. which of the following completes the proof? alternate interior angles theorem converse of the alternate interior angles theorem converse of the same-side interior angles theorem same-side interior angles theorem

Answers: 2
Similar questions

Mathematics, 01.07.2019 12:30, LuluMathLover101
Answers: 1

Mathematics, 16.07.2019 02:30, corrineikerd
Answers: 2

Mathematics, 24.07.2019 09:00, dooboose15
Answers: 1

Mathematics, 16.09.2019 14:00, johnsonwhitney2
Answers: 2
Do you know the correct answer?
Spencer wrote the following paragraph proof showing that rectangles are parallelograms with congruen...
Questions in other subjects:


Mathematics, 31.03.2020 00:52


Biology, 31.03.2020 00:52



Chemistry, 31.03.2020 00:52